TD4 - Compilation séparée et makefile
Compilation séparée et makefile
Durée : 1h30
Elisabeth Ranisavljevic - Inès de Courchelle
Attention :
À chaque étape de programmation, vous devez vérifier si le programme :
- Compile sans warning
- Obtient les résultats attendus
- Avant de coder, il faut écrire un algo avec un papier et un stylo !

Rappels
Pour compiler un programme, on utilise l’instruction suivante :
gcc -Wall exo.c -o nomExecutablePour executer un programme, on utilise l’instruction suivante :
./nomExecutableProblèmatique
Écrire un programme qui propose, via un menu, les actions suivantes (les prototypes de fonctions/procédures vous sont donnés):
- Affichage d’un sapin : void affichageSapin(int n);
- Rang de la factorielle : int maxFact(int k);
- Nombre d’Armstrong : void estArmstrong(int n);
- Affichage binaire : void binaire(int n);
- Coefficients binômiaux : int coefBin(int n, int p);
Avant de commencer
Créer l’arborescence suivante :
Créer le makefile permettant de compiler et d’exécuter les 3 fichiers
Objectif
Mise en garde
- Tester chaque fonctionnalité petit à petit avant de créer le MENU
- Vérifier qu’elles marchent et qu’elles ne générent pas d’erreur !
Le sapin
/* Auteur : xxxxxxxxx */
/* Date : xxxxxxxx */
/* Résumé : procédure qui prend en paramètre un nombre n puis affiche un sapin de noël en utilisant uniquement les caractères ASCII */
/* Entrée(s) : La taille du sapin */
/* Sortie(s) : aucunes */
void sapin (int n);Cette procédure affiche un sapin en utilisant uniquement les caractères ascii.
Tout d’abord, le haut du sapin se dessine par un triangle isocèle en utilisant uniquement les caractères “*” et ” ” (espace). Ensuite, le tronc est dessiné par un carré (3x3) de “@”. L’entier n permet de connaitre la taille du haut du sapin. Voici un exemple pour n = 5:
*
***
*****
*******
*********
@@@
@@@
@@@Rang de la factorielle
/* Auteur : xxxxxxx */
/* Date : xxxxxxxxxxx */
/* Résumé : fonction qui calcule pour un entier k donné, le plus grand entier n tel que n ! ≤ k . Attention, Ne pas faire trop de multiplications */
/* Entrée(s) : un entier */
/* Sortie(s) : un entier */
int rangFactorielle (int k);Cette fonction doit calculer, pour un entier k donné, le plus grand entier n tel que n! ≤ k.
Nombre d’Armstrong
/* Auteur : xxxxxxx */
/* Date : xxxxxxxxxxx */
/* Résumé : prédicat qui permet d'identifier si un nombre, passé en paramètre est un nombre d’Armstrong */
/* Entrée(s) : Le nombre à tester (strictement positif) */
/* Sortie(s) : 1 => vrai 0 => faux */
int estArmstrong (int nb);Cette fonction doit définir si un nombre (saisi par l’utilisateur) est un nombre d’Armstrong. C’est-à-dire que ce nombre est égal à la somme des cubes des chiffres qui le composent.
Exemple : 153 : 13 + 53 + 33 = 1 + 125 + 27 = 153
Quelques nombres d’Armstrong : 1, 153, 370, 371, 407.
TIPS utiliser les modulos et la division pour isoler chaque chiffre du nombre !
Affichage binaire
/* Auteur : xxxxxxx */
/* Date : xxxxxxxx */
/* Résumé : procédure qui affiche un nombre base 10 en base 2 (binaire)*/
/* Entrée(s) : Le nombre à convertir (strictement positif) */
/* Sortie(s) : aucunes */
void affichageBinaire(int nb);Cette procédure prend en paramètre un entier naturel n et affiche son écriture binaire (en base 2).
Attention Afficher petit à petit le binaire dans la procédure. NE PAS une chaîne de caractères !
Coefficients binômiaux
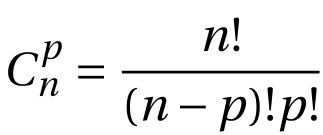
- Quelle est la complexité de cette fonction ? Quelle est la valeur maximale calculable ?
- Cette fonction calcule le coefficient binômial. Proposer une (ou plusieurs) autre(s) méthode(s) (non récursives) moins coûteuse et permettant de calculer des valeurs beaucoup plus grandes.